叶序双1 顾文彬1 张鹏翔1 阳天海2
1.解放军理工大学工程兵工程学院,南京210007;2.工程兵技术装备研究所。无锡214035)
摘自《工程爆破文集》第七辑
摘 要 对装药在无限水介质中爆炸所出现的第二个压力波现象进行了初步讨论;并根据数值模拟和试验研究结果,对其传播规律进行了探讨。
关键词 无限水介质,爆炸,第二个压力波,冲击波
对装药在无限水介质中爆炸的数值模拟和试验研究中,我们注意到了第二个压力波的出现。
图l是有多个压力峰值(如图1中PA、PB、PC)的实测波形。其实验条件为:水深d=5.8m,水质为淡水,装药距水底的距离H=3.8m,装药距水面的距离H1=2m;装药为球形TNT,其质量C=36kg,密度为1600kg/m3,半径r=0.175m。测点距装药中心的距离r=3.57m。
图1 有第二个压力波的实测曲线
Fig.1 curvetestedwithtl-e second
图1中tB-tA=0.013ms、tC-tA=0.0656ms;气泡脉动周期可用式[1]
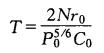 式(1)中,N=4350,取r0=0.175m,Po=105Pa,Co=1500m/s,可算得T=0.0692ms,与tC- tA 的值较相近。从压力峰值出现的时间上来看,pC应为气泡首次脉动引起的二次压力波;pB 在 pC加在之前出现,为区别于二次压力波我们称此波为第二个压力波。
图2为单个装药在无限水介质中爆炸,不同时刻水中冲击波传播的情况数值模拟的结果(关于数值模拟研究将另文详细介绍)。球形装药水中爆炸情况下,爆炸产物压缩水介质形成水中冲击波之后,立刻在爆炸产物中形成逆气流运动压缩波。该压缩波在爆心处汇聚、再反射为更强的压缩波,顺气流运动。反射压缩波到达产物与水的分界面时,由于产物此前的快速膨胀,使其冲击阻抗远小于水的冲击阻抗,该压缩波在界面处发生透射,形成冲击波传入水中,即形成第二个压力波。该压力波在爆炸冲击波(第一个冲击波)扰动之后的水介质中向前传播。[2,3]从图2(e)、(f)中可以清楚地看到爆炸冲击波之后的第二个压力波的压力等值面。
图2 单个装药在无限水中爆炸冲击波的传播
Fig.2 Shock waves’propagation subjected to explosion of one charge in infinite water
图3(a)表示距爆心0.76m处空间点压力的计算曲线。从图中可以看出,此处只有爆炸冲击波的作用,而第二个压力波才刚刚到达。图3(b)所示为距爆心1.975m处空间点压力的计算曲线。图中的第二波峰即是第二个压力波在已扰动水介质中作用的结果,它随冲击波之后球形向前传播,传播速度小于冲击波传播速度。
分析表l可知,在库尔公式适用的范围(0.637<r<=r/ <12.821)内,峰值压
力数值计算结果与库尔公式计算结果的相对误差最大为8.1%,最小为3.5%。
图3 第二个压力波的形成和传播
Fig.3 formation and propagation of the second pressure wave
表1 数值计算结果与库尔公式计算结果的比较
Table 1 Comparison between the results of numerical simulation and that by formula P.cole
|
距装药中心距离r/m |
/r |
经验式计算Pm/MPa |
数值计算Pm/MPa |
相对误差/% |
|
2.156 |
1.532 |
86.29 |
81.382 |
-5.7 |
|
2.509 |
1.316 |
72.71 |
70.17 |
-3.5 |
|
2.905 |
1.137 |
61.60 |
59.160 |
-4.0 |
|
3.486 |
0.945 |
50.13 |
47.751 |
-4.8 |
|
3.930 |
0.84 |
43.78 |
40.279 |
-8.0 |
|
4.134 |
0.799 |
41.35 |
38.00 |
-8.1 |
|
4.604 |
0.717 |
36.61 |
33.804 |
-7.6 |
|
4.822 |
0.685 |
34.75 |
32.101 |
-7.5 |
|
5.067 |
0.652 |
32.85 |
30.206 |
-8.0 |
由数值计算结果,应用最小二乘法多元线性回归,拟合出水中冲击波峰值压力计算公式:
当0.167<r<2时(r为比例距离,m/kg1/3),
(2)式的相关系数为0.9219。
图4为根据库尔公式和拟合公式(2)作出的Pm~r曲线。图中实线代表库尔公式计算结果,虚线代表拟合公式(2)计算结果,比例距离严范围为0.4≤r≤2.5。由图可知,数值模拟的水中冲击波的峰值压力,随测点距离的衰减规律,与库尔公式的计算结果比较一致。
在0.36<r<1.25内,根据数值计算数据,模拟的第二个压力波叠加压力峰值随比例距离尹(m/kg1/3)的衰减规律为:
(3)式的相关系数为0.8902。
由图1知:深水中r=1.08处实测峰值压力、第二压力波迭加后的压力峰值分别为:44.8MPa、36.47MPa;根据式(2)、(3)计算的相应值分别为45.0 MPa、36.5MPa,表明r=1.08处公式计算值与实测值较相近。图5中为实测数据与根据式(3)计算的模拟曲线。由图5可看出模拟曲线与实测数据较相近。
(来源:中国爆破网)
|